논리회로를 이용한 덧셈기 만들기 (책 code chapter 11-12 정리)

시작하기 이전에

1. 논리회로와 전기회로는 등가성을 지닌다. (논리회로의 값으로 전기회로를 구성하면 논리회로와 동일하게 작동한다.)
2. 논리회로는 수학에서의 집합의 개념으로 접근이 가능하다. (중고등학교때 배운 합집합, 교집합 등을 여기에 써먹을 줄이야.)
3. 논리게이트를 사용하여 전기회로(등가성을 지니므로 논리회로라고 봐도 무방)가 특정 조건에서 특정 동작을 수행하도록 조작할 수 있다.
4. 이러한 조작방법은 크게 6가지로 각각 AND, OR, NAND, NOR, XOR 게이트와 인버터(NOT 게이트)로 구체화할 수 있다.

 

시작하기 이전에 하나 더 / 집합과 논리회로의 관계

교과서에서 보던 일반적인 벤다이어그램

• A∩B (A와 B의 교집합/ A와 B가 공유하는 가운데 부분) = AND게이트 [설명 : A도 참이고 B도 참인 것]
• A∪B (A와 B의 합집합/ A 혹은 B가 가진 모든 부분) = OR게이트 [설명 : A가 참이거나 B가 참인 것]
• A^c (A의 여집합/ A가 가지고 있지 않은 모든 부분) = 인버터(NOT게이트) [설명 : 전체집합 중 A가 아닌 것]
• U (전체집합/ 모집합) = 1 [설명 : 참인 것. 집합에서는 모든 것]
• Ø (공집합) = 0 [설명 : 거짓인 것. 집합에서는 없는 것]
• NAND, NOR, XOR 등은 위의 식을 조합해서 생성함

 

논리회로

1. AND게이트

박스 안에 선 뚜룩뚜룩 나 있는 것은 전자석이다.

AND	0	1
0	0	0
1	0	1

AND게이트는 두개의 입력이 모두 참일 때 동작하는 게이트다. 두개 중 한개의 입력이 거짓이면 작동하지 않는다. (AND게이트를 표시하는 기호는 그림의 우측 하단과 같다.)

 

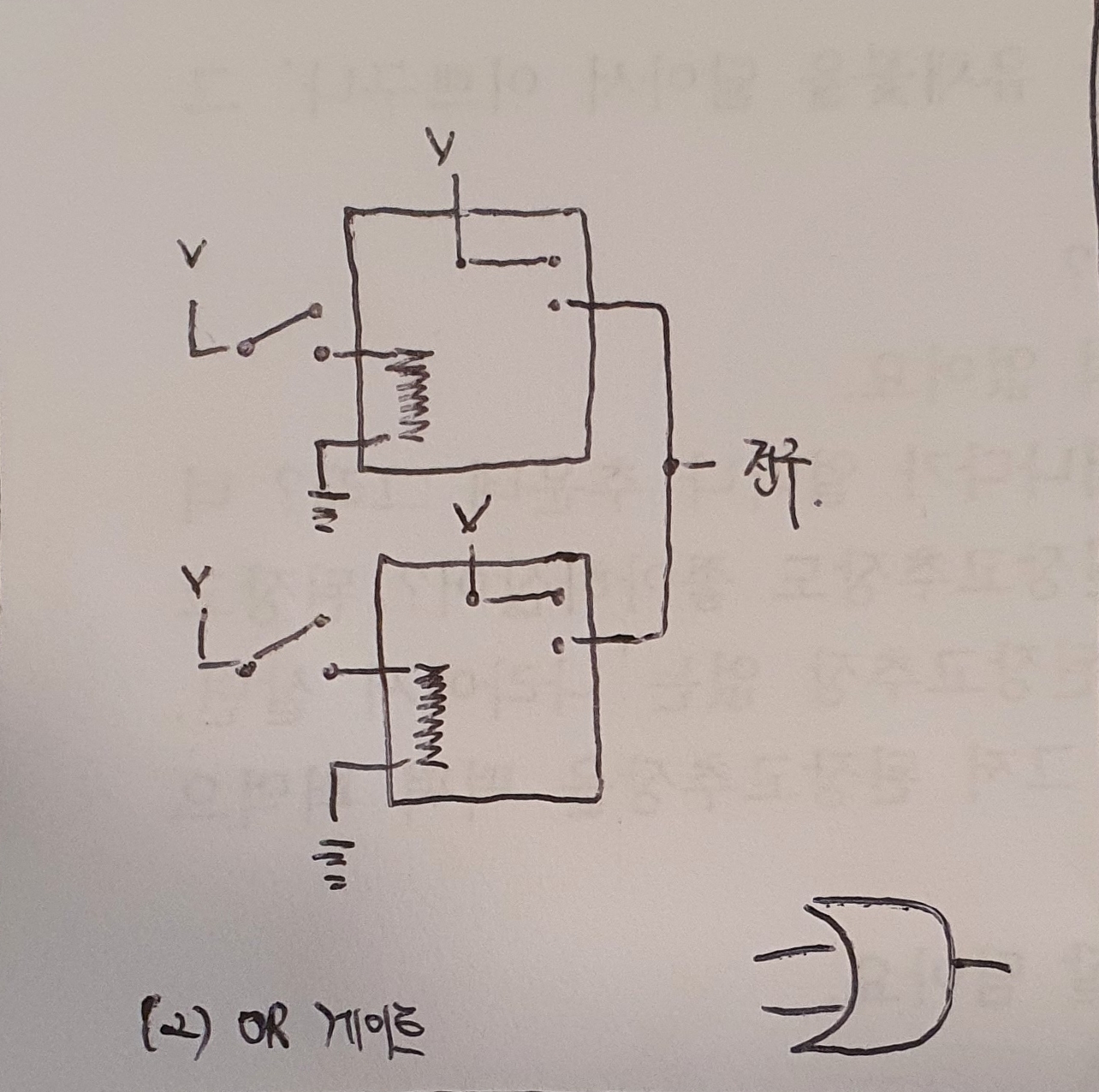
2. OR게이트

OR	0	1
0	0	1
1	1	1

OR게이트는 두개의 입력 중 한개의 입력만 참이면 동작하는 게이트다. 두개 모두 거짓인 경우에만 작동하지 않는다. (OR게이트의 기호는 역시 그림 우측 하단의 것과 같다. 너무 뚱뚱하게 그려졌다 ㅎ)

 

3. 인버터 (NOT게이트) / NAND게이트 / NOR게이트

인버터는 전구의 위치가 위의 경우와 반대로 되어 있다.

NOT	0	1
0	1	0
1	0	0

인버터(NOT게이트)는 입력값이 없을 때 동작하는 게이트다. 입력이 0이라면 1이, 입력이 1이라면 0이 출력된다. 인버터는 다른 게이트와 섞어서 사용되기도 하는데 인버터가 AND게이트와 사용되면 NAND게이트가, OR게이트와 사용되면 NOR게이트가 된다. 기호로는 작은 동그라미를 그리는 것으로 표현하고 NAND게이트와 NOR게이트 같은 경우는 AND, OR게이트 출력부에 작은 동그라미를 그리는 것으로 표현된다. NAND게이트와 NOR게이트의 출력식은 다음과 같다.

NAND	0	1	구 분 선	NOR	0	1
0	1	1		0	1	0
1	1	0		1	0	0

 

본격, 덧셈기 만들기

자, 이제 덧셈기를 만들 준비가 끝났다. 물론 매우 원시적(?)인 장치로 모니터로 값을 출력해주지도 키보드를 통해 값을 입력해주지도 않는다. 그러나 이것은 컴퓨터를 만드는 대단히 기념비적이고 상징적인 장치이다.

 

값이 커지면 식이 너무(너무너무너무너무너무....) 복잡해지니 최대한 간단한 계산을 통해 실습을 진행해보고자 한다. 자, 역사적인 순간이다. 나는 논리회로를 통해 2+3의 값, 즉 5를 도출해 볼 것이다.

 

Step 1. 이진수로 바꾸기

우선 2와 3의 값을 이진수로 바꿔보자. 이진수는 0과 1, 두개의 값만을 지닌다. 즉 이진수에서 숫자 2는 10이다. (간단히 생각하면 1 이상의 값이 나오면 자릿수가 올라간다고 보면 된다. 십진수에서는 10을 기준으로 자릿수가 올라가고, 이진수는 2를 기준으로 자릿수가 올라가는거다.) 그러면 우리는 이런 결과를 낼 수 있다. 십진수 2는 이진수 10, 십진주 3은 이진수 11이다. 보기 쉽게 아래에 한번 더 적어보자.

• 2 = 10
• 3 = 11

자 이번에는 이진수의 덧셈표를 가져와보자. 십진수는 덧셈표가 (상대적으로) 길고 복잡하겠지만 이진수에서는 아니다. 덧셈표는 다음과 같다.

 

이 식을 이용해 10과 11의 덧셈을 구하면 다음과 같다. 십진수와 마찬가지로 일의자리에서부터 연산을 진행해보자.

• [일의 자리] 1+0 = 1 (합의 값 =1 / 자리올림 값 = 0)
• [2의 자리] 1+1 = 10 (합의 값 =0 / 자리올림 값 = 1)
• [2²의 자리] 1 (2의 자리올림 값이 1이었기에)
• 결과/ 10 + 11 = 101 (십진수 5 = 이진수 101)

 

Step 2. 논리게이트 구축하기

위의 덧셈표의 '합의 표'와 '자리이동 표'에 주목해주길 바란다. 뭔가 어디선가 봤던 표 같지 않은가? 맞다, 앞서 살펴본 논리게이트의 표와 상당히 유사해 보인다. 자, 거의 다 왔다. 이제 덧셈표를 논리게이트로 편입해보자.

 

1. 우선 자리올림표부터 진행해볼까. 위로 올라가 자리올림표가 같은 모양의 논리게이트를 찾는다. AND게이트다. 자리올림표는 간단하게 AND게이트로 표현이 가능하다.
2. 합의 표는 조금 어렵다. 언뜻 보기에는 OR게이트와 유사해 보이지만 하나 다른 부분이 있다. 바로 1과 1이 만나는 부분이 OR게이트에서는 1로 되어 있지만 '합의 표'에서는 0으로 되어 있다. 이를 해결하기 위해서는 기존의 게이트를 조합하여 '합의 표'와 같은 결과값을 만들어야 한다. 이제 아까 소개하지 않았던 새로운 논리게이트, OR게이트와 NAND게이트, 그리고 AND게이트를 결합한 XOR게이트를 소개한다.

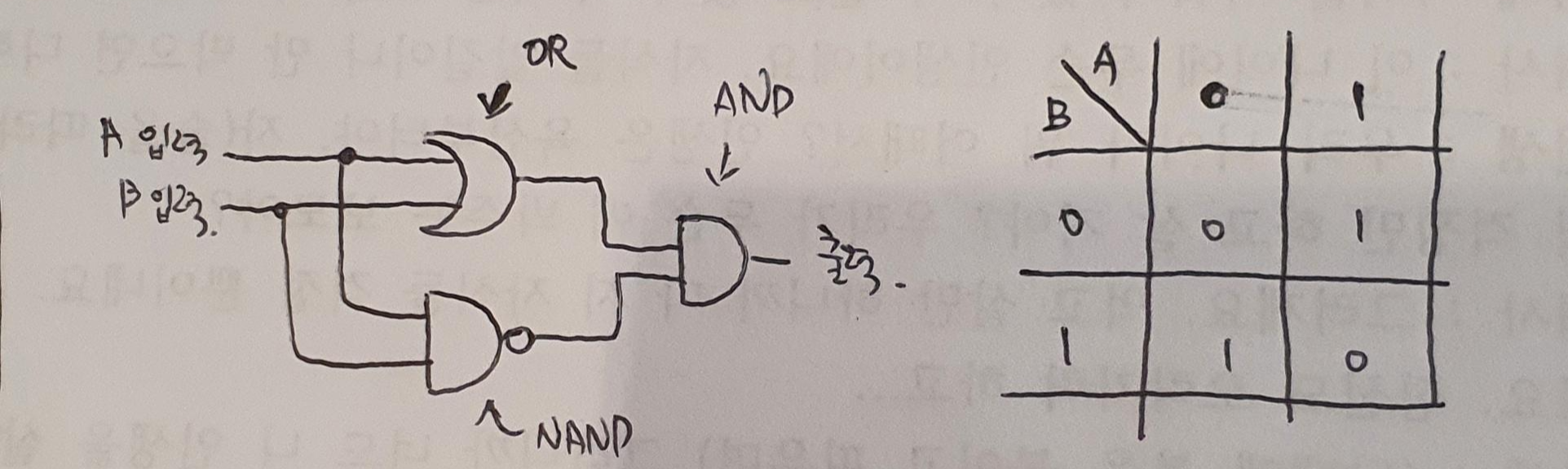
마지막 게이트 XOR게이트이다. '합의 표'와 결과값이 완전히 동일한 것을 확인할 수 있다. 이제, AND게이트와 XOR게이트를 이용하여 논리회로식을 만들 수 있다.

 

Step 3. 이진수로 바꾼 값을 논리식에 편입하기

거의 다 왔다. 이제 AND게이트와 XOR게이트를 적절히 구성하여 입력에 따라 '합의 표'와 '자리올림 표'가 작동하는 기적을 만나보자. 

위의 그림 중 왼쪽은 AND게이트와 XOR게이트를 이용하여 합의 값과 자리올림 값을 출력하는 논리식이다. 오른쪽은 왼쪽의 식을 간략화하여 표현한 것이다. (같은 논리식임!!!)

 

그런데, 진짜 아쉽다. 하나가 남았다. 마지막 하나. 정말 아쉽게도 반가산기를 통해서는 아랫자리에서 올라온 자리올림값을 처리할 수 없다. A와 B의 입력값만을 고려하기 때문이다. 반가산기만을 통해서는 제대로된 덧셈값을 얻을 수 없다. 마지막 과정은 제 3의 변수인 '이전 자리올림 값'을 포함할 수 있는 궁극의 논리식을 만드는 것이다.

축하한다, 이진수의 '합의 값'과 '자리올림 값'을 출력할 수 있음은 물론이고, '이전자리의 올림 값'도 고려할 수 있는 이진수 덧셈 연산의 최종단계인 전가산기를 만들었다. 이제 이 전가산기를 사용하기만 하면 된다. 각 자리마다 전가산기 한개를 배치하면 어렵지 않게 10과 11의 합을 계산할 수 있다. 이제 최종단계, 실제 계산으로 가보자.

 

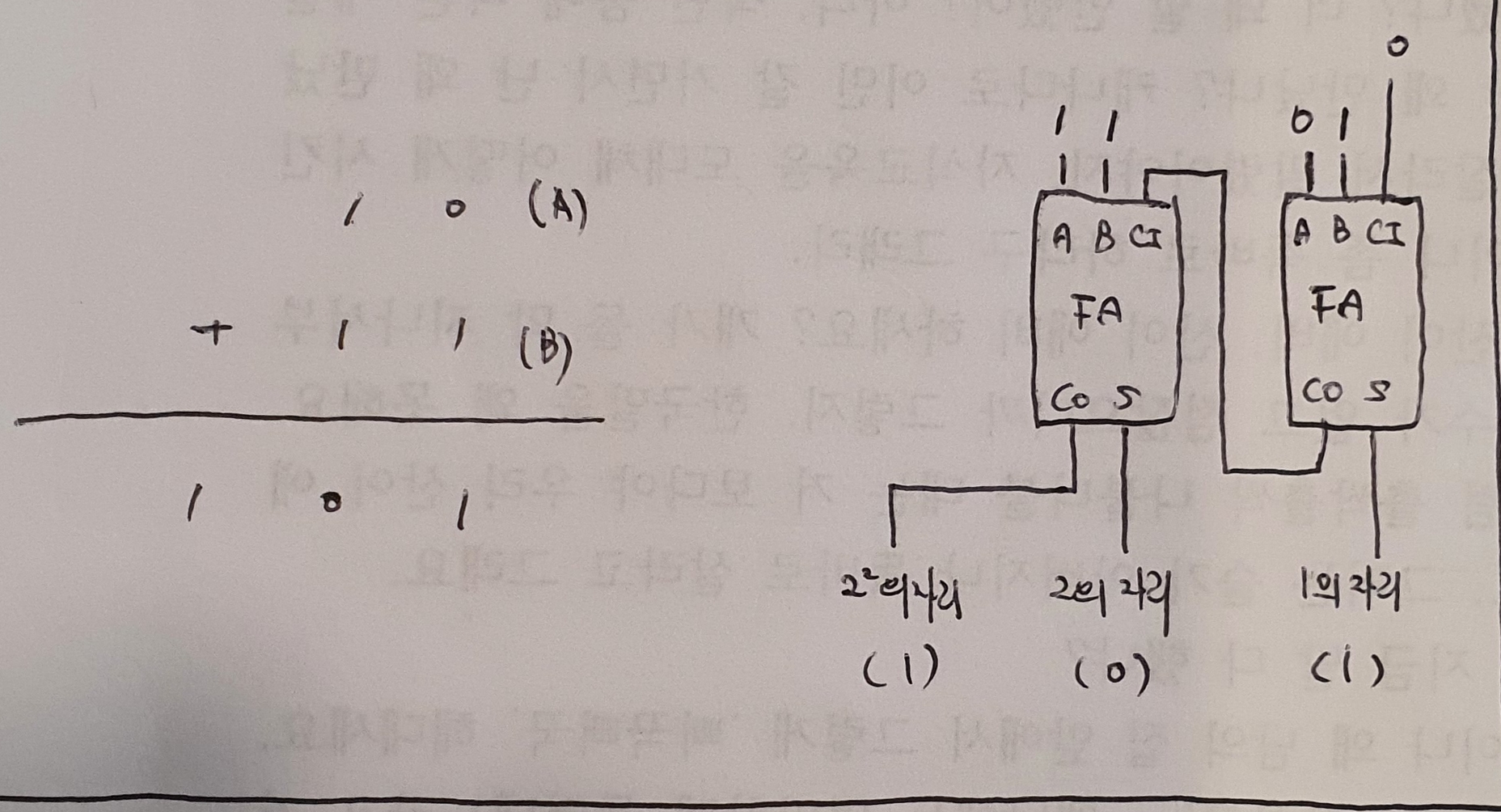
좌측은 이진수 계산법을 이용하여 직접 계산을 하였을 경우, 우측은 가상의 논리식을 이용하여 계산을 하였을 경우이다. (FA는 전가산기를 의미하고 1의 자리의 CI값이 0인 것은 1의 자리 아래의 자리는 없기 때문이다.) 보이는 바와 같이 값이 동일하다는 것을 알 수 있다. 비록 사고실험에 불과하지만 실제로 장비를 구해 전기회로를 구축한다 해도 같은 결과를 보일 것이다. 원시적인 컴퓨터를 만들었다. (컴퓨터라고 부를 수 있을지 모르겠지만;;;)

 

---

오늘은 책 CODE의 chapter 11과 12장을 복습해보았다. 머릿속으로 입력된 지식이 정리되지 않은 듯 하여 지식을 정리하고자 글을 작성하기 시작했는데 생각보다 쓸 부분이 많아서 힘들었다...; 그래도 이진수를 이용하여 식의 합을 구하는 것, 그리고 그것을 논리회로로 만드는 방법을 제대로 복습한 것 같아서 의미 깊다.

 

책을 읽다보니 일반적인 그래픽카드 하나에는 10억개 이상의 릴레이가 들어있다고 한다. (릴레이는 '인버터'의 그림처럼 생긴 친구들...이다. 똑같은 신호를 증폭시켜주는 역할을 수행한다. 전기회로를 열거나 닫는 구실을 하는 기기이기도 하다!) 10억개라니.... 경이롭다는 생각을 했다.